> Tamilnadu State board 10th Maths Solutions Chapter 1 Relations and Functions Exercise 1.3 ( EX 1.3 ) ~ Kalvikavi - Educational Website - Question Paper
Home » » Tamilnadu State board 10th Maths Solutions Chapter 1 Relations and Functions Exercise 1.3 ( EX 1.3 )

Tamilnadu State board 10th Maths Solutions Chapter 1 Relations and Functions Exercise 1.3 ( EX 1.3 )

1 comment

 Tamilnadu State board 10th Maths Answers Chapter 1 Relations and Functions Exercise 1.3 ( EX 1.3 )

You can Download and practice Tamilnadu state board 10th Maths Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Reduced Syllabus and score more marks in your Public examinations and assignment writing work 


Tamilnadu State board 10th Maths Solutions Chapter 1 Relations and Functions Exercise 1.3 ( EX 1.3 )

  • Question 1.

Let f = {(x, y)|x, y ∈ N and y = 2x} be a relation on N. Find the domain, co-domain and range. Is this relation a function?

  • Solution:

F = {(x, y)|x, y ∈ N and y = 2x}

x = {1, 2, 3,…}

y = {1 × 2, 2 × 2, 3 × 2, 4 × 2, 5 × 2 …}

R = {(1, 2), (2, 4), (3, 6), (4, 8), (5, 10),…}

Domain of R = {1, 2, 3, 4,…},

Co-domain = {1, 2, 3…..}

Range of R = {2, 4, 6, 8, 10,…}

Yes, this relation is a function.

  • Question 2.

Let X = {3, 4, 6, 8}. Determine whether the relation R = {(x, f(x))|x ∈ X, f(x) = x² + 1} is a function from X to N ?

  • Solution:

x = {3,4, 6, 8}

R = ((x, f(x))|x ∈ X, f(x) = X² + 1}

f(x) = x² + 1

f(3) = 3² + 1 = 10

f(4) = 4² + 1 = 17

f(6) = 6² + 1 = 37

f(8) = 8² + 1 = 65

Tamilnadu State board 10th Maths Answers Chapter 1 Relations and Functions Exercise 1.3 ( EX 1.3 )

R = {(3, 10), (4, 17), (6, 37), (8, 65)}

R = {(3, 10), (4, 17), (6, 37), (8, 65)}

Yes, R is a function from X to N.

  • Question 3.

Given the function

f : x → x2 – 5x + 6, evaluate

(i) f(-1)

(ii) f(2 a)

(iii) f(2)

(iv) f(x – 1)

  • Answer:

f(x) = x2 – 5x + 6

(i) f (-1) = (-1)2 – 5 (-1) + 6 = 1 + 5 + 6 = 12

(ii) f (2a) = (2a)2 – 5 (2a) + 6 = 4a2 – 10a + 6

(iii) f(2) = 22 – 5(2) + 6 = 4 – 10 + 6 = 0

(iv) f(x – 1) = (x – 1)2 – 5 (x – 1) + 6

= x2 – 2x + 1 – 5x + 5 + 6

= x2 – 7x + 12

  • Question 4.

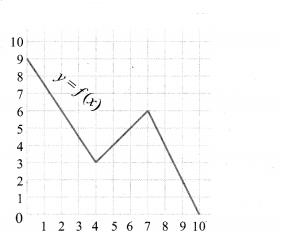
A graph representing the function f(x) is given in figure it is clear that f(9) = 2.

Tamilnadu State board 10th Maths Answers Chapter 1 Relations and Functions Exercise 1.3 ( EX 1.3 )

(i) Find the following values of the function

(a) f(0)

(b) f(7)

(c) f(2)

(d) f(10)

(ii) For what value of x is f (x) = 1?

(iii) Describe the following

(i) Domain

(ii) Range.

(iv) What is the image of 6 under f?

  • Solution:

From the graph

(a) f(0) = 9

(b) f(7) = 6

(c) f(2) = 6

(d) f(10) = 0

(ii) At x = 9.5, f(x) = 1

(iii) Domain = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10}

= {x |0 < x < 10, x ∈ R}

Range = {x|0 < x < 9, x ∈ R}

= {0, 1, 2, 3, 4, 5, 6, 7, 8, 9}

(iv) The image of 6 under f is 5.

  • Question 5.

Let f(x) = 2x + 5. If x ≠ 0 then

 find `frac{f(x+2)-f(2)}{x}`

Solution:
Given f(x) = 2x + 5, x ≠ 0
Tamilnadu State board 10th Maths Answers Chapter 1 Relations and Functions Exercise 1.3 ( EX 1.3 )

  • Question 6.

A function fis defined by f(x) = 2x – 3
(i) find `frac{f(0)+f(1)}{2}`
(ii) find x such that f(x) = 0.
(iii) find x such that f(x) = x.
(iv) find x such that f(x) = f(1 – x).
Solution:
Given f(x) = 2x – 3
(i) find `frac{f(0)+f(1)}{2}`
f(0) = 2(0) – 3 = -3
f(1) = 2(1) – 3 = -1
`frac{f(0)+f(1)}{2}=\frac{-3-1}{2}=\frac{-4}{2}`

(ii) f(x) = 0
⇒ 2x – 3 = 0
2x = 3
x = `frac{3}{2}`

(iii) f(x) = x
⇒ 2x – 3 = x ⇒ 2x – x = 3
x = 3

(iv) f(x) = f(1 – x)
2x – 3 = 2(1 – x) – 3
2x – 3 = 2x – 2x – 3
2x + 2x = 2 – 3 + 3
4x = 2
x = `frac{2}{4}`

x= `frac{1}{2}`

    Question 7.

An open box is to be made from a square piece of material, 24 cm on a side, by cutting equal squares from the corners and turning up the sides as shown in figure. Express the volume V of the box as a function of x.

Tamilnadu State board 10th Maths Answers Chapter 1 Relations and Functions Exercise 1.3 ( EX 1.3 )

  • Solution:

Volume of the box = Volume of the cuboid
= l × b × h cu. units
Here l = 24 – 2x
b = 24 – 2x
h = x
∴ V = (24 – 2x) (24 – 2x) × x
= (576 – 48x – 48x + 4x²)x
V = 4x³ – 96x² + 576x

  • Question 8.

A function f is defined bv f(x) = 3 – 2x . Find x such that f(x2) = (f(x))2.

  • Solution:

f(x) = 3 – 2x
f(x²) = 3 – 2x³


  • Question 9.

A plane is flying at a speed of 500 km per hour. Express the distance d travelled by the plane as function of time r in hours.

  • Answer:

Speed of the plane = 500 km/hr
Distance travelled in “t” hours
= 500 × t (distance = speed × time)
= 500 t

  • Question 10.

The data in the adjacent table depicts the length of a woman’s forehand and her corresponding height. Based on this data, a student finds a relationship between the height (y) and the forehand length(x) as y = ax + b, where a, b are constants.

Tamilnadu State board 10th Maths Answers Chapter 1 Relations and Functions Exercise 1.3 ( EX 1.3 )

(i) Check if this relation is a function.
(ii) Find a and b.
(iii) Find the height of a woman whose forehand length is 40 cm.
(iv) Find the length of forehand of a woman if her height is 53.3 inches.

  • Solution:

(i) Given y = ax + b …………. (1)
The ordered pairs are R = {(35, 56) (45, 65) (50, 69.5) (55, 74)}
∴ Hence this relation is a function.

Tamilnadu State board 10th Maths Answers Chapter 1 Relations and Functions Exercise 1.3 ( EX 1.3 )

⇒ 65 = 45(.9) + b
⇒ 65 = 40.5 + b
⇒ b = 65 – 40.5
⇒ b = 24.5
∴ a = 0.9, b = 24.5
∴ y = 0.9x + 24.5
(iii) Given x = 40 , y = ?
∴ (4) → y = 0.9 (40) + 24.5
⇒ y = 36 + 24.5
⇒ y = 60.5 inches
(iv) Given y = 53.3 inches, x = ?
(4) → 53.3 = 0.9x + 24.5
⇒ 53.3 – 24.5 = 0.9x
⇒ 28.8 = 0.9x
⇒ x = `frac{28.8}{0.9}` =32 cm
∴ When y = 53.3 inches, x = 32 cm
Share:

1 Comments:

Popular Posts