10th Maths Answers Chapter 2 Numbers and Sequences Ex 2.2
You can Download 10th Maths Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.
1.For what values of natural number n, 4n can end with the digit 6?
Answer:
4ⁿ = (2 × 2)ⁿ = 2ⁿ × 2ⁿ
2 is a factor of 4ⁿ.
So, 4n is always even and end with 4 and 6.
When n is an even number say 2, 4, 6, 8 then 4ⁿ can end with the digit 6.
Example:
4² = 16
4³ = 64
4⁴ = 256
4⁵ = 1,024
4⁶ = 4,096
4⁷ = 16,384
4⁸ = 65, 536
4⁹ = 262,144
2.If m, n are natural numbers, for what values of m, does 2ⁿ × 5ᵐ ends in 5?
Answer:
2ⁿ is always even for any values of n.
[Example. 2² = 4, 2³ = 8, 2⁴ = 16 etc]
5m is always odd and it ends with 5.
[Example. 5² = 25, 5³ = 125, 5⁴ = 625 etc]
But 2ⁿ × 5ᵐ is always even and end in 0.
[Example. 2³ × 5³ = 8 × 125 = 1000
2² × 5² = 4 × 25 = 100]
∴ 2ⁿ × 5ᵐ cannot end with the digit 5 for any values of m.
3.Find the H.C.F. of 252525 and 363636.
Answer:
To find the H.C.F. of 252525 and 363636
Using Euclid’s Division algorithm
363636 = 252525 × 1 + 111111
The remainder 111111 ≠ 0.
∴ Again by division algorithm
252525 = 111111 × 2 + 30303
The remainder 30303 ≠ 0.
∴ Again by division algorithm.
111111 = 30303 × 3 + 20202
The remainder 20202 ≠ 0.
∴ Again by division algorithm
30303 = 20202 × 1 + 10101
The remainder 10101 ≠ 0.
∴ Again using division algorithm
20202 = 10101 × 2 + 0
The remainder is 0.
∴ 10101 is the H.C.F. of 363636 and 252525.
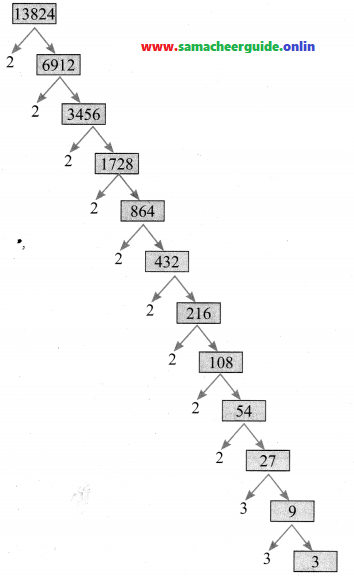
4.If 13824 = 2ᵃ × 3ᵇ then find a and b.
Answer:
If 13824 = 2ᵃ × 3ᵇ
Using the prime factorisation tree
13824 = 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 3 × 3 × 3
= 2⁹ × 3³ = 2ᵃ × 3ᵇ
∴ a = 9, b = 3.
5.If p₁x₁ × p₂x₂ × p₃x₃ × p₄x₄ = 113400 where p₁, p₂, p₃, p₄ are primes in ascending order and x₁, x₂, x₃, x₄ are integers, find the value of P₁ ,P₂, P₃, P₄ and x₁, x₂, x₃, x₄.
Answer:
If p₁x₁ × p₂x₂ × p₃x₃ × p₄x₄ = 113400
p₁, p₂, p₃, P₄ are primes in ascending order, x₁, x₂, x₃, x₄ are integers.
using Prime factorisation tree.
113400 = 2 × 2 × 2 × 3 × 3 × 3 × 3 × 5 × 5 × 7
= 23 × 34 × 52 × 7
= p₁x₁ × p₂x₂ × p₃x₃ × p₄x₄
∴ p₁= 2, p₂ = 3, p₃ = 5, p₄ = 7, x₁ = 3, x₂ = 4, x₃ = 2, x₄ = 1.
6.Find the L.C.M. and H.C.F. of 408 and 170 by applying the fundamental theorem of arithmetic.
Answer:
408 and 170.
408 = 2³ × 3¹ × 17¹
170 = 2¹ × 5¹ × 17¹
∴ H.C.F. = 2¹ × 17¹ = 34.
To find L.C.M, we list all prime factors of 408 and 170, and their greatest exponents as follows.
∴ L.C.M. = 2³ × 3¹ × 5¹ × 17¹
= 2040.
7.Find the greatest number consisting of 6 digits which is exactly divisible by 24, 15, 36?
Answer:
To find L.C.M of 24, 15, 36
24 = 2³ × 3
15 = 3 × 5
36 = 2² × 3²
∴ L.C.M = 2³ × 3² × 5¹
= 8 × 9 × 5
= 360
If a number has to be exactly divisible by 24, 15, and 36, then it has to be divisible by 360. Greatest 6 digit number is 999999.
Common multiplies of 24, 15, 36 with 6 digits are 103680, 116640, 115520, …933120, 999720 with six digits.
∴ The greatest number consisting 6 digits which is exactly divisible by 24, 15, 36 is 999720.
8.What is the smallest number that when divided by three numbers such as 35, 56 and 91 leaves remainder 7 in each case?
Answer:
Find the L.C.M of 35, 56, and 91
35 – 5 × 7 56
56 = 2 × 2 × 2 × 7
91 = 7 × 13
L.C.M = 23 × 5 × 7 × 13
= 3640
Since it leaves remainder 7
The required number = 3640 + 7
= 3647
The smallest number is = 3647
9.Find the least number that is divisible by the first ten natural numbers.
Answer:
The least number that is divisible by the first ten natural numbers is 2520.
Hint:
1,2, 3,4, 5, 6, 7, 8,9,10
The least multiple of 2 & 4 is 8
The least multiple of 3 is 9
The least multiple of 7 is 7
The least multiple of 5 is 5
∴ 5 × 7 × 9 × 8 = 2520.
L.C.M is 8 × 9 × 7 × 5
= 40 × 63
= 2520






0 Comments:
Post a Comment